こんにちは、タナカです。
この記事では、ある線に対して、ある点からの垂線を描画する方法を説明します。
- ある線に対して、ある点からの垂線を描画する方法がわかる
1. 垂線を引くとは
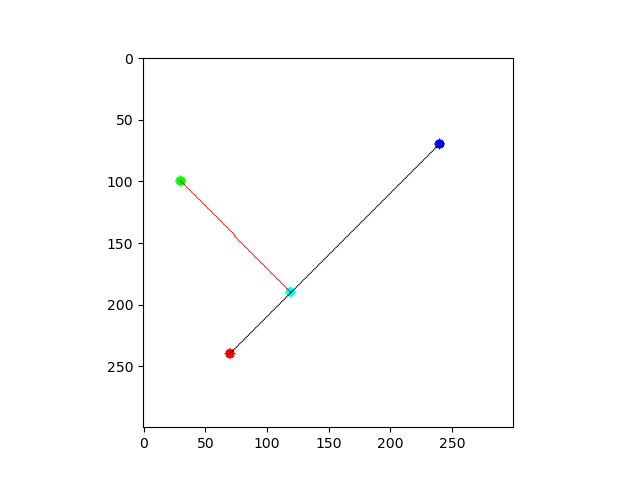
ある2点(p1, p2)を結んだ線に対して、点pからの垂線をopencvを使って描画します。この時与えられているのは、p1とp2、pのみです。
最終的な垂線のイメージが赤線になります。
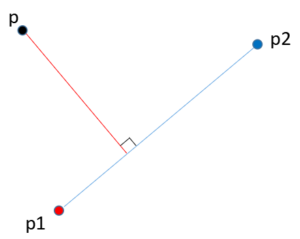
2. 画像について
画像に線や円などを描画する前に、まず画像の特性を理解しておく必要があります。
pythonのopencvを使って図形を描画する方法の記事でも書きましたが、画像はピクセルと呼ばれる四角の集まりで構成されており、その四角一つひとつに座標(x, y)を持っています。
そのため、ベクトルを使って考えることができます。
3. 垂線を描画する手順
まず初めに、垂線を描画する手順を示します。後ほど図とコードの両方を示しながら詳細に説明します。
- 1. ベクトルで考える
- 2. 線と垂線が交わる点を求める
- 3. 垂線を描画する
3-1. ベクトルで考える
前述したとおり、画像は座標情報をもっているため、ベクトルで考えることができます。ベクトルで考える場合、原点o(0, 0)を可視化するとわかりやすいので書いてます。
もちろん原点oは省略しても、どこに書いても大丈夫です。

コードで書くとこのようになります。300×300の真っ白な画像を準備して、その画像の上に各点と線を描画しています。
import numpy as np
import matplotlib.pyplot as plt
import cv2
height = 300
width = 300
# 真っ白な300x300の画像
white = np.ones([height, width, 3], dtype = np.uint8) * 255
# p1とp2の座標を下記とする
p1 = (70, 240)
p2 = (240, 70)
p = (30, 100)
# o = (0, 0) 省略
# v1, v2を作成する
# np.array(o)は0ベクトルなので省略
v1 = np.array(p1) # - np.array(o)
v2 = np.array(p2) # - np.array(o)
u = np.array(p) # - np.array(o)
# 点を描画
cv2.circle(white, p1 , 4, (255, 0, 0), -1) # p1
cv2.circle(white, p2 , 4, (0, 0, 255), -1) # p2
cv2.circle(white, p, 4, (0, 255, 0), -1) # u
# 線を描画
cv2.line(white, p1, p2, (0, 0, 0), 1)
# 図の可視化
plt.imshow(white)
plt.show()
3-2. 線と垂線が交わる点を求める
次に線と垂線が交わる点を求めていきたいと思います。交点は次の手順に沿って求めます。
- p1とp2の単位ベクトルeを求める
- ベクトルuとベクトルv1の差分ベクトルuv1を求める
- 差分ベクトルuv1と単位ベクトルeの内積を求める
- 交点ベクトルmを求める
3-2-1. p1とp2の単位ベクトルeを求める
単位ベクトルとは大きさが1のベクトルのことです。ベクトルなので向きを持っています。
単位ベクトルeは下記の式で求めることができます。
$$e = \frac{v2 – v1}{\sqrt{v2^2 + v1^2}}$$
また、単位ベクトルを図で示すとこのようになります。
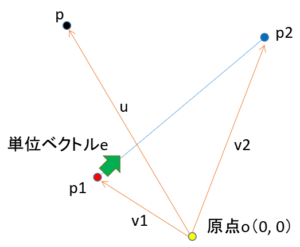
コードで書くとこのようになります。np.linalg.norm()でp1とp2の距離(スカラー)を求めることができます。
# 単位ベクトルe
e = (v2 - v1) / np.linalg.norm(v2 - v1)
3-2-2. ベクトルuとベクトルv1の差分ベクトルを求める
次にベクトルuとベクトルv1の差分ベクトルを求めます。図で示すと水色の矢印にあたるベクトルです。
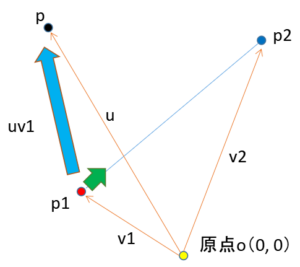
コードで書くとこのようになります。
# 差分ベクトルuv1
uv1 = u - v1
3-2-3. ベクトルuv1と単位ベクトルeの内積を求める
ベクトルuv1と単位ベクトルeの内積を計算することで図で示した赤線の大きさ(スカラー)を求めることができます。こちらのページが参考になりました。
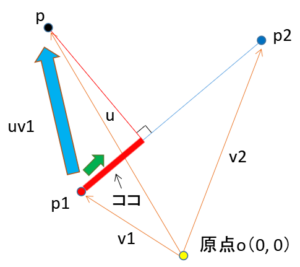
内積はnp.dotを使うことで簡単に求めることができます。
# 内積
scalar = np.dot(uv1, e)
3-2-4. 交点ベクトルmを求める
最後に交点ベクトルmを求めていきます。
先ほど求めた内積はただの大きさなので、単位ベクトルeをかけることで新たなベクトルを作ります。これは、点p1から点tのベクトルになります。
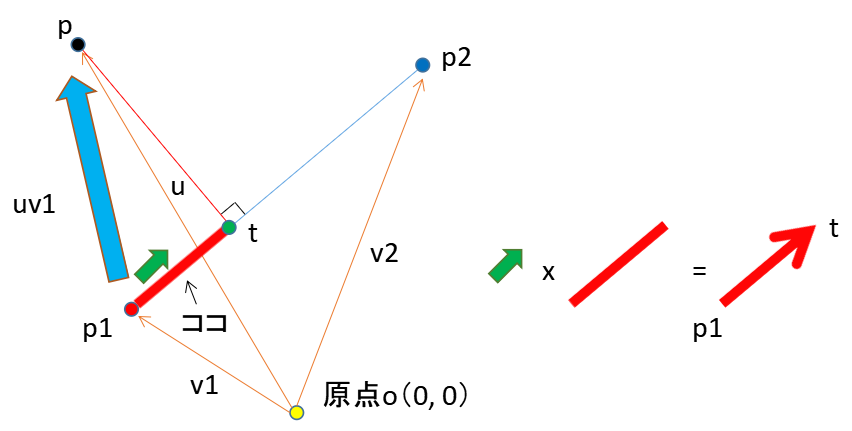
ここまで求めることができれば、交点ベクトルmを求めることができます。
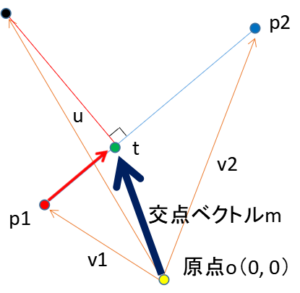
交点ベクトルmは原点oから点tまでのベクトルなので、コードで書くとこのようになります。
cv2.circle()では浮動小数点のまま座標を指定することができないため、「int(m[0])やint(m[1])」と整数値にしています。
# 交点ベクトルm
# np.dot(uv1, e): 内積
# e: 単位ベクトル
m = np.dot(uv1, e) * e + v1
# 交点ベクトルの描画
cv2.circle(white, (int(m[0]), int(m[1])), 4, (0, 255, 255), -1)
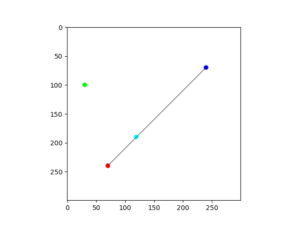
3-3. 垂線を描画する
交点ベクトルmを求めることができれば、あとはベクトルuと交点ベクトルmを結べば、垂線を描画することができます。
cv2.line(white, tuple(u), (int(m[0]), int(m[1])), (255, 0, 0), 1)
これである点から、ある線に対して垂線を描画する方法の説明は以上になります。
まとめ
pythonのopencvとnumpyを使って垂線を描画する方法について説明しました。
画像は、ピクセルと呼ばれるもので構成されており、その一つひとつが座標情報を持つため、ベクトルで考えることができます。
最後に今回使用したコードを示します。
import numpy as np
import matplotlib.pyplot as plt
import cv2
height = 300
width = 300
# 真っ白な300x300の画像
white = np.ones([height, width, 3], dtype = np.uint8) * 255
# p1とp2の座標下記とする
p1 = (70, 240)
p2 = (240, 70)
p = (30, 100)
o = (0, 0)
# v1, v2, uを作成する
# np.array(o)は0ベクトルなので省略
v1 = np.array(p1) # - np.array(o)
v2 = np.array(p2) # - np.array(o)
u = np.array(p) # - np.array(o)
# 単位ベクトルe
e = (v2 - v1) / np.linalg.norm(v2 - v1)
# 差分ベクトルuv1
uv1 = u - v1
# 内積
# scalar = np.dot(uv1, e)
# 交点ベクトルm
m = np.dot(uv1, e) * e + v1
# 点を描画
cv2.circle(white, p1 , 4, (255, 0, 0), -1) # p1
cv2.circle(white, p2 , 4, (0, 0, 255), -1) # p2
cv2.circle(white, p, 4, (0, 255, 0), -1) # u
# 交点ベクトルmを描画
cv2.circle(white, (int(m[0]), int(m[1])), 4, (0, 255, 255), -1)
# 線を描画
cv2.line(white, p1, p2, (0, 0, 0), 1)
cv2.line(white, tuple(u), (int(m[0]), int(m[1])), (255, 0, 0), 1)
# 図の可視化
plt.imshow(white)
plt.show()