こんにちは、タナカです。
この記事では、ポアソンブレンディングを用いて画像合成する方法を解説します。
この記事を書こうと思った理由は、機械学習用にキズや穴などの不良箇所を画像合成してNG画像を生成したいと考えたからです。
機械学習をするうえでは、どうしても学習枚数を増やす必要があり、その一つの手段として画像合成があります。もちろん、そのまま合成画像が使えるかは検証の余地があります。
今回、画像の合成アルゴリズムにポアソンブレンディングを利用しました。コードはこちらを参考にさせていただき、自分なりの解釈を含め解説します。
このような一般的な画像を使って解説します。

srcは合成させたい画像、targetは合成先となります。単純合成の場合は、srcとtargetの境界を考慮せず合成するため、不自然さが残ります。
それに対して、ポアソンブレンディングは勾配に基づいて画像を合成しています。
このポアソンブレンディングのアルゴリズムをできるだけわかりやすく解説します。
ではいきましょう。
- 画像合成アルゴリズムの内容がわかる
1. 画像合成とは
画像合成とは、複数の画像を1枚の画像に合成することを言います。単純に合成させた画像がこちらになります。

それぞれの境界をなにも考慮していないため、不自然な画像となっていることがわかります。この単純合成するコードはこのようになります。
import cv2
import numpy as np
import math
def simple_coposition(src, target, mask):
img = target * (1.0 - mask) + (src * (mask))
img = img.astype(np.uint8)
return img
# src: 合成したい画像
src = cv2.imread('people-gbe1f8f837_640.jpg')
h, w = src.shape[:2]
ratio = w / h
src = cv2.resize(src, (math.ceil(ratio * 256), 256))[:, 50:50+256]
# target: 合成先
target = cv2.imread('apple-1834639_640.jpg')
target = cv2.resize(target, dsize = (256, 256))
# mask: マスク
mask = np.zeros(src.shape, dtype = np.uint8)
cv2.ellipse(mask, ((135, 130), (50, 100), 0), (255, 255, 255), thickness = -1)
mask = mask / 255
sc = simple_coposition(src, target, mask)
単純合成用にマスクを3次元にしています。ポアソンブレンディングで使うためには、1次元にする必要があるのでご注意ください。
# mask = mask / 255
mask = cv2.cvtColor(mask, cv2.COLOR_BGR2GRAY) / 255.0
次からポアソンブレンディングによる画像合成について説明していきます。
2. ポアソンブレンディングによる合成
ポアソンブレンディングとは、画像合成アルゴリズムの一つです。ポアソン方程式を解くことで元の勾配を保ちながら,境界部分が連続となる合成画像を推定する
合成画像をI、ソース画像(合成したい画像)をS、ターゲット画像をTとし、合成領域をΩ、合成境界を∂Ω、とすると今回解くべきポアソン方程式がこちらになります。この境界値問題を解くことによって合成画像を生成することができます。
\begin{eqnarray}
{\Delta I(x, y) = \Delta S(x, y) \quad in \quad \Omega} \\
{I(x, y) = T(x, y) \quad on \quad \partial \Omega}
\end{eqnarray}
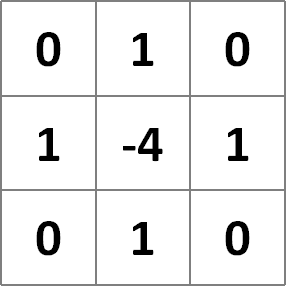
∆(ラプラシアン)は2次微分のことで画像ではこのようなフィルターとして知られています。つまりこのフィルターを通した画像は、2次微分されたと同意ということです。
先ほどの合成領域Ωや合成境界∂Ωは図で示すとこのような場所を言います。
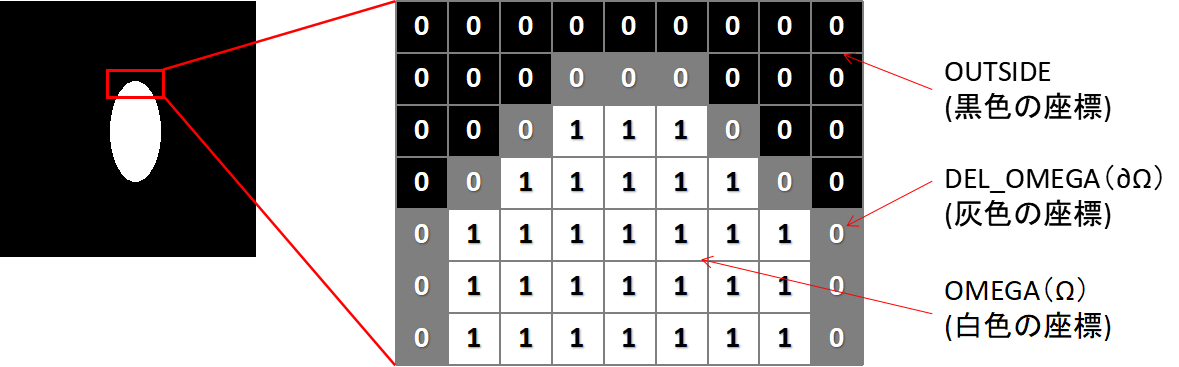
これはマスク画像の一部を拡大したもので、合成される領域がΩ、その境界部分が∂Ωになります。
境界や合成領域を判断する処理をコードで書くとこのようになります。
OMEGA = 0
DEL_OMEGA = 1
OUTSIDE = 2
def point_location(index, mask):
if in_omega(index, mask) == False:
return OUTSIDE
if edge(index, mask) == True:
return DEL_OMEGA
return OMEGA
def in_omega(index, mask):
return mask[index] == 1
def edge(index, mask):
# OUTSIDEの場合
if in_omega(index, mask) == False:
return False
for pt in get_surrounding(index):
if in_omega(pt, mask) == False:
return True # DEL_OMEGAの場合
return False # OMEGAの場合
point_location関数で、その座標がΩなのか∂Ωなのか、それとも全く関係ないアウトサイドなのかを判断しています。
ポアソン方程式では、画像中の座標の位置がΩなのか、∂Ωなのかで処理が変わります。
例えば、下図の点Aと点Bでは、ラプラシアンを適用した際に結果が変わるということです。具体的に言うと点Bでは一つ上と一つ左のピクセルが∂Ωに干渉していますが、点Aでは干渉していないということです(0は結果に影響しないため無視)。
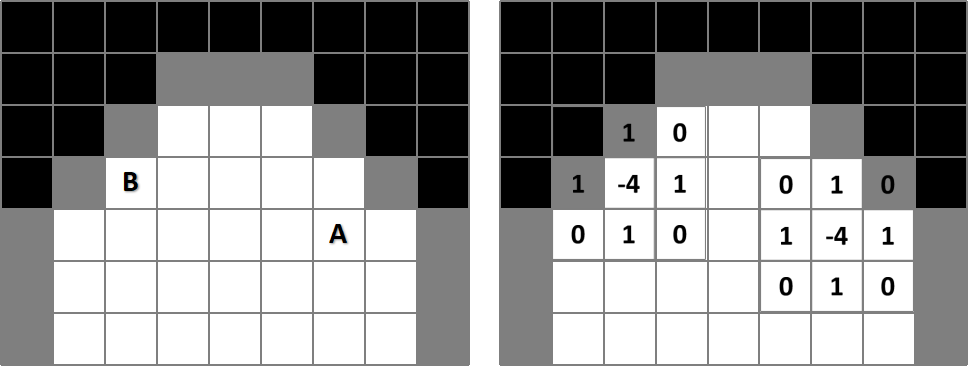
合成する箇所以外は勾配の計算が不要なため、このラプラシアンは合成領域の座標上のみで適用されます。
また、先ほどのポアソン方程式の境界値問題を解くことで合成画像I(x, y)を生成できると書きましたが、実際にはこの連立方程式を共役勾配法で解くことによってI(x, y)を求めることができます。共役勾配法はこちらの記事が参考になりました。

Aは疎行列になります。疎行列とは行列の要素の大部分が0の行列のことです。これがラプラシアンに該当します。
xは求めたい合成行列の画素値になります。
bはソース画像にラプラシアンを適用した値になります。∂Ωの場合のみ、ターゲット画像の画素値がbに減算されます。
疎行列やラプラシアンを適用する処理をコードで書くとこのようになります。
import numpy as np
from scipy.sparse import linalg, lil_matrix
import scipy
# ラプラシアン
def lap_at_index(src, index):
i, j = index
value = (1 * src[i+1, j]) + (1 * src[i-1, j]) + (1 * src[i, j+1]) + (1 * src[i, j-1]) - (4 * src[i, j])
return value
def mask_indicies(mask):
# zero以外の座標情報を取得(合成画像の座標を取得)
nonzero = np.nonzero(mask)
nonzeros = zip(nonzero[0], nonzero[1])
nonzero_list = []
for nonzero in nonzeros:
nonzero_list.append(nonzero)
return nonzero_list
# 注目座標の周囲4マス
def get_surrounding(index):
i, j = index
return [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
# 疎行列の作成
def poisson_sparse_matrix(points):
# 合成座標の数
N = len(points)
# 疎行列
A = lil_matrix((N, N))
for i, index in tqdm.tqdm(enumerate(points)):
# 対角は-4を代入
A[i, i] = -4
for x in get_surrounding(index):
if x not in points:
continue
j = points.index(x)
# -4の周囲4マスに1を代入
A[i, j] = 1
return A
疎行列は合成領域が大きくなればなるほど、生成に時間がかかります。大きさにもよりますが、結構かかります。疎行列の生成についてもっと効率的な方法があればご教授いただければ幸いです。
最終的に合成画像を生成するコードはこのようになります。
def process(src, target, mask):
# 合成座標
indicies = mask_indicies(mask)
# 合成座標の数
N = len(indicies)
# 疎行列
A = poisson_sparse_matrix(indicies)
# b行列の初期化
b = np.zeros(N)
for i, index in tqdm.tqdm(enumerate(indicies)):
# ラプラシアンの適用
b[i] = lap_at_index(src, index)
# 境界の場合
if point_location(index, mask) == DEL_OMEGA:
# 周囲4pixの座標を取得
for pt in get_surrounding(index):
# オメガでない場合
if in_omega(pt, mask) == False:
b[i] -= target[pt]
x = linalg.cg(A, b)
composite = np.copy(target).astype(int)
# Place new intensity on target at given index
for i,index in enumerate(indicies):
composite[index] = x[0][i]
return composite
img = [process(src[:,:,i], target[:,:,i], mask) for i in range(3)]
共役勾配法はscipyというライブラリを使うと簡単に記述することができます。
x = linalg.cg(A, b)
最後にポアソンブレンディングで合成した画像を示します。

おまけ
画像合成するだけなら正直opencvのseamlessCloneという関数を使えばもっと簡単に実施することができます。ありえないくらい簡単で高速です。実用的なのはこっちかな。
import cv2
import numpy as np
import matplotlib.pyplot as plt
import math
# src: 合成したい画像
src = cv2.imread('people-gbe1f8f837_640.jpg')
h, w = src.shape[:2]
ratio = w / h
src = cv2.resize(src, (math.ceil(ratio * 256), 256))[:, 50:50+256]
# target: 合成先
target = cv2.imread('apple-1834639_640.jpg')
target = cv2.resize(target, dsize = (256, 256))
# mask: マスク
mask = np.zeros(src.shape, dtype = np.uint8)
cv2.ellipse(mask, ((135, 130), (50, 100), 0), (255, 255, 255), thickness = -1)
# 画像合成
img = cv2.seamlessClone(src, target, mask, (135, 130), cv2.MIXED_CLONE)
plt.imshow(img)
plt.show()
opencvでは合成したい場所を指定できるのと、合成手法を選ぶことが可能です。本当にすごい。
まとめ
今回はポアソンブレンディングのアルゴリズムを解説しました。
画像合成はディジタル画像処理の分野でかなり実用性のある技術だと思っています。理論や概念を理解したいと思ったので一から記述して勉強しました。
おそらく、分かりづらい箇所や説明が不足している部分があると思いますが、ご容赦ください。
ディジタル画像処理の分野は本当におもしろい。