こんにちは、タナカです。
この記事では、画像上に描画された2本の直線の交点を求める方法を解説します。
- 2本の直線の交点を求める方法がわかる
- pythonを使って交点を求めるコードが書けるようになる
1. 交点の確認
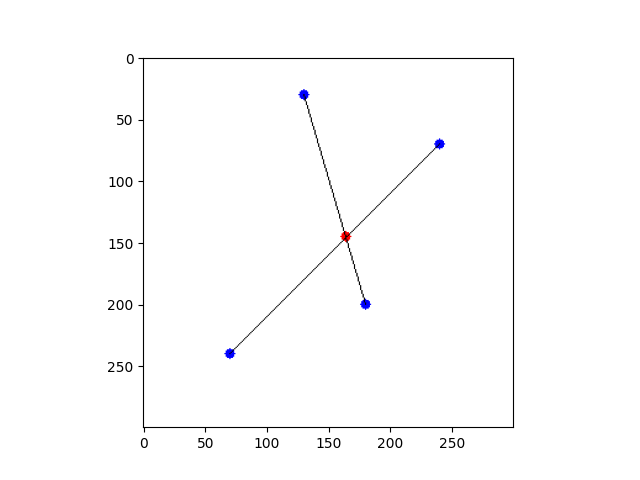
図に示したような直線と直線の交点をpythonを使って求めたいと思います。

2. 交点を求める手順
交点を求める手順は下記のとおりです。後ほど、図とコードの両方を示しながら説明していきます。
- 1. ベクトルで考える
- 2. 二次方程式を立てる
- 3. 二次方程式から変数ua, ubを求める
- 4. 交点を求める
2-1. ベクトルで考える
画像上に描画されたものはベクトルで考えることができます。ベクトルで考える場合、原点o(0, 0)を可視化するとわかりやすいので書いています。
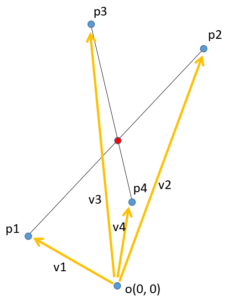
それぞれp1、p2、p3、p4までのベクトルをv1、v2、v3、v4としています。コードで書くとこのようになります。
import numpy as np
import matplotlib.pyplot as plt
import cv2
height = 300
width = 300
# 真っ白な300x300の画像
white = np.ones([height, width, 3], dtype = np.uint8) * 255
# p1とp2の座標を下記とする
p1 = (70, 240)
p2 = (240, 70)
p3 = (130, 30)
p4 = (180, 200)
# o = (0, 0) 省略
# v1, v2を作成する
# np.array(o)は0ベクトルなので省略
v1 = np.array(p1) # - np.array(o)
v2 = np.array(p2) # - np.array(o)
v3 = np.array(p3) # - np.array(o)
v4 = np.array(p4) # - np.array(o)
# 点を描画
cv2.circle(white, p1 , 4, (0, 0, 255), -1) # p1
cv2.circle(white, p2 , 4, (0, 0, 255), -1) # p2
cv2.circle(white, p3 , 4, (0, 0, 255), -1) # p3
cv2.circle(white, p4 , 4, (0, 0, 255), -1) # p4
# 線を描画
cv2.line(white, p1, p2, (0, 0, 0), 1)
cv2.line(white, p3, p4, (0, 0, 0), 1)
# 図の可視化
plt.imshow(white)
plt.show()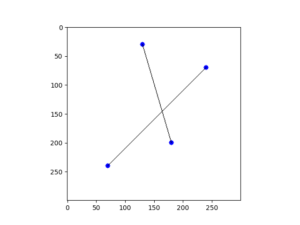
2-2. 二次方程式を立てる
交点までのベクトルは各ベクトルを使って2つの式を立てることができます。
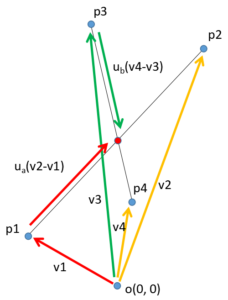
$$Va = V1 + u_a(V2 – V1)$$ $$Vb = V3 + u_b(V4 – V3)$$
uaとubはそれぞれV2-V1とV4-V3の長さを調整する値になります。Va=Vbとなる点を考えて、uaとubを導きます。
$$V1 + u_a(V2 – V1) = V3 + u_b(V4 – V3)$$
さらに各ベクトルをx成分とy成分に分けて書くとこのようになります。
$$x1 + u_a(x2 – x1) = x3 + u_b(x4 – x3)$$ $$y1 + u_a(y2 – y1) = y3 + u_b(y4 – y3)$$
2-3. 二次方程式から変数ua, ubを求める
先ほどの2つの式から、uaとubについて解くと下記になります。
$$u_a = \frac{(x4 – x3)(y1 – y3) – (y4 – y3)(x1 – x3)}{(y4 – y3)(x2 – x1) – (x4 – x3)(y2 – y1)}$$ $$u_b = \frac{(x2 – x1)(y1 – y3) – (y2 – y1)(x1 – x3)}{(y4 – y3)(x2 – x1) – (x4 – x3)(y2 – y1)}$$
例えば、交点ベクトルのx成分、y成分はこのようになります。
$$x = x1 + u_a(x2 – x1)$$ $$y = y1 + u_a(y2 – y1)$$
2-4. 交点を求める
先ほどの値を使って実際に交点を求めるコードを書いていきます。
先ほどのコードに追記するコードがこちらになります。
# 成分に分ける
x1, y1 = v1
x2, y2 = v2
x3, y3 = v3
x4, y4 = v4
# 分子、分母の値
denominator = (y4 - y3) * (x2 - x1) - (x4 - x3) * (y2 - y1)
nua = (x4 - x3) * (y1 - y3) - (y4 - y3) * (x1 - x3)
nub = (x2 - x1) * (y1 - y3) - (y2 - y1) * (x1 - x3)
# ua, ubを求める
ua = nua / denominator
ub = nub / denominator
# 交点ベクトルのx, y
x = x1 + ua * (x2 - x1)
y = y1 + ua * (y2 - y1)
# 交点を描画
cv2.circle(white, (int(x), int(y)), 4, (255, 0, 0), -1)
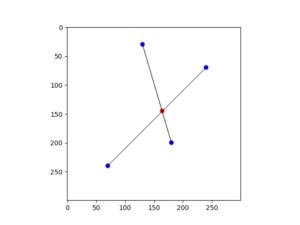
まとめ
直線と直線の交点をpythonを使って求めてみました。交点を求める応用例として、【PyQt5】画像の範囲外にマウスが来た時の挙動を考えるという記事があるので参考にしてみてください。
ベクトルの考え方ってかなり面白いですよね。特に画像処理では、ほぼベクトルの概念で説明することができます。
こういう技術は様々なところで使用できるので、ぜひ参考にしてみてください。