※当サイトではアフィリエイト広告を利用しています。

画像処理

【opencv】回転後の座標を取得する方法

こんにちは、タナカです。

この記事では、opencvとnumpyを使って回転後の座標を取得する方法を紹介します。

image-rotation
この記事の内容

回転後の座標を取得する方法がわかる

目次

1. 回転画像

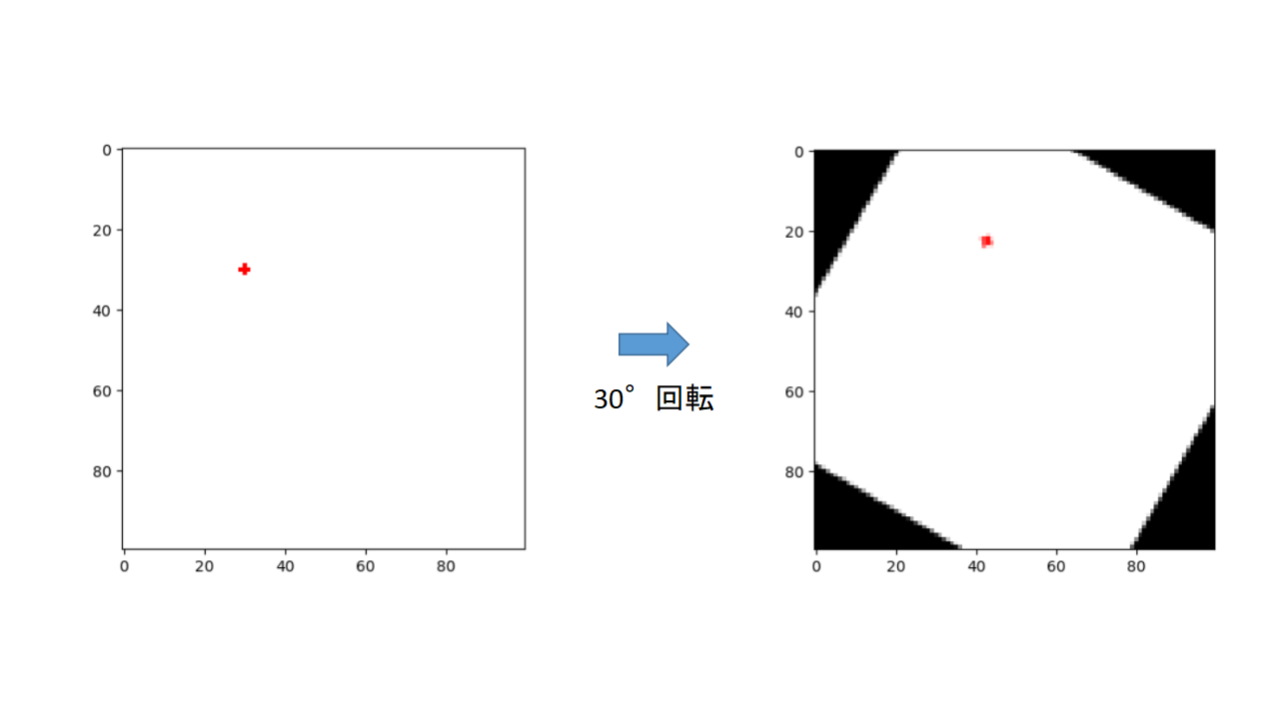
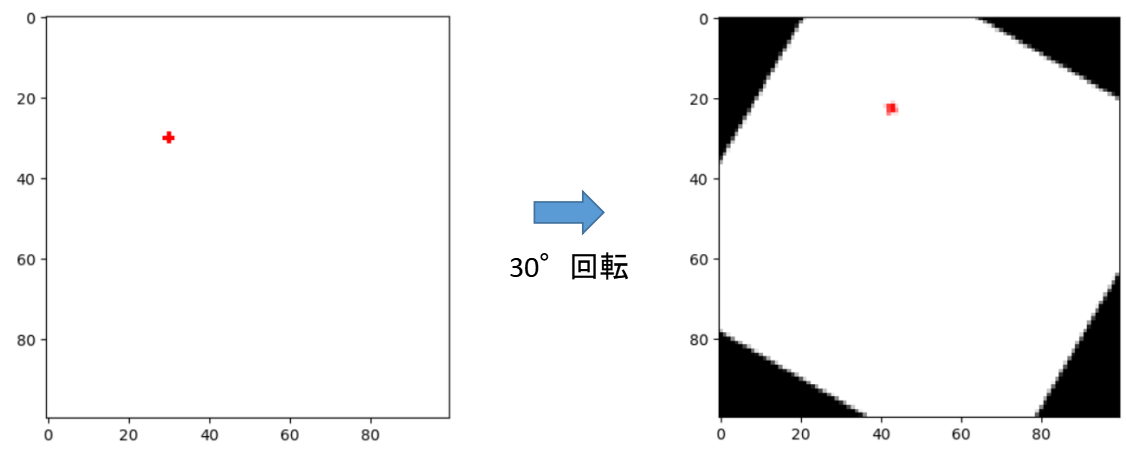
opencvを使って30°画像を回転させたものがこちらになります。

rotation30

その時のコードがこちらになります。

import cv2
import matplotlib.pyplot as plt
import numpy as np

# 真っ白画像
white = np.ones((100, 100, 3), dtype = np.uint8) * 255

# point
p1 = np.array([30, 30])

# pointの描画
cv2.circle(white, tuple(p1), 1, (255, 0, 0), -1)

# 角度
deg = 30

# 回転マトリクスの作成
height, width = white.shape[:2]

# 画像中心
center = np.array([width // 2, height // 2])

# 回転マトリクス
rot_m = cv2.getRotationMatrix2D(tuple(center), -deg, 1)
rot_img = cv2.warpAffine(white, rot_m, (width, height))

# 画像の表示
plt.imshow(rot_img)
plt.show()

 

事前に真っ白の画像を準備して、そこに赤点を描画しています。

画像の回転はopencvのgetRotationMatrix2Dを使っており、画像の中心を軸として回転させる処理を記述しています。

2. 回転後の座標取得

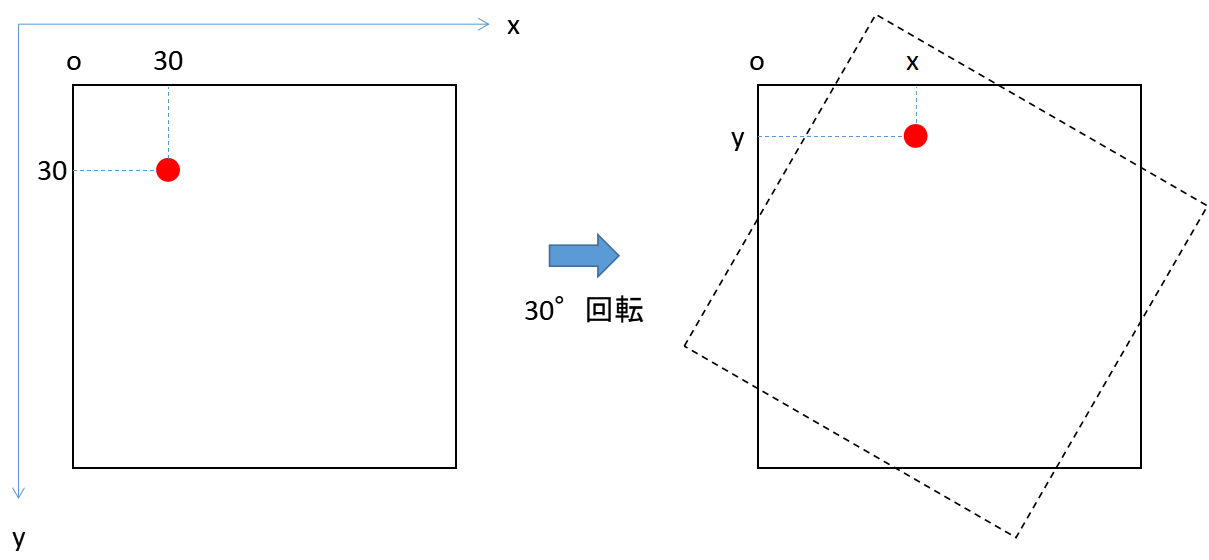
先ほどの画像では、元々(x=30, y=30)の座標にあった赤点が30度回転することで、座標が変わっていることがわかると思います。

この回転後の座標は回転行列と元々の座標との内積を取ることで求めることができます。

式で書くとこのようになります。

$$
\left( \begin{array}{cc} x’\\ y’\\ \end{array} \right) = \left(\begin{array}{cc} cos{θ} & -sin{θ} \\ sin{θ} & cos{θ} \\ \end{array} \right) \left( \begin{array}{cc} x\\ y\\ \end{array} \right)
$$

また、コードで書くとこのような関数を作ることができます。

def rotCoordinate(v, rad):
    # 回転行列
    rot_m = np.array([[np.cos(rad), -np.sin(rad)],
                      [np.sin(rad), np.cos(rad)]])
    return np.dot(rot_m, v)

 

引数であるvが中心から赤点(p1)までのベクトルで、rad（ラジアン）が回転角度になります。

今回は画像の中心を軸として回転させているため、中心からのベクトルを考える必要があります。（どこを軸とするかで変わります）

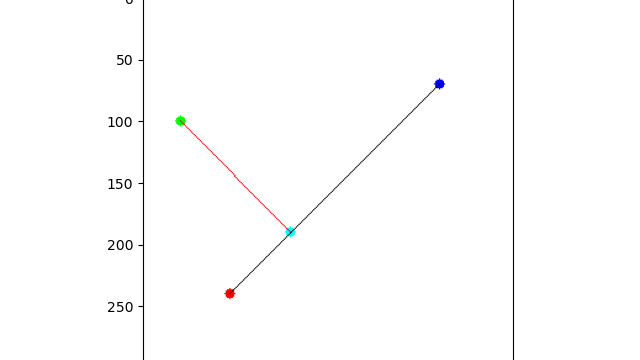
図で示すとこのようになります。ベクトルで考えるときは原点を適当に決めてあげるとイメージしやすいので書いています。

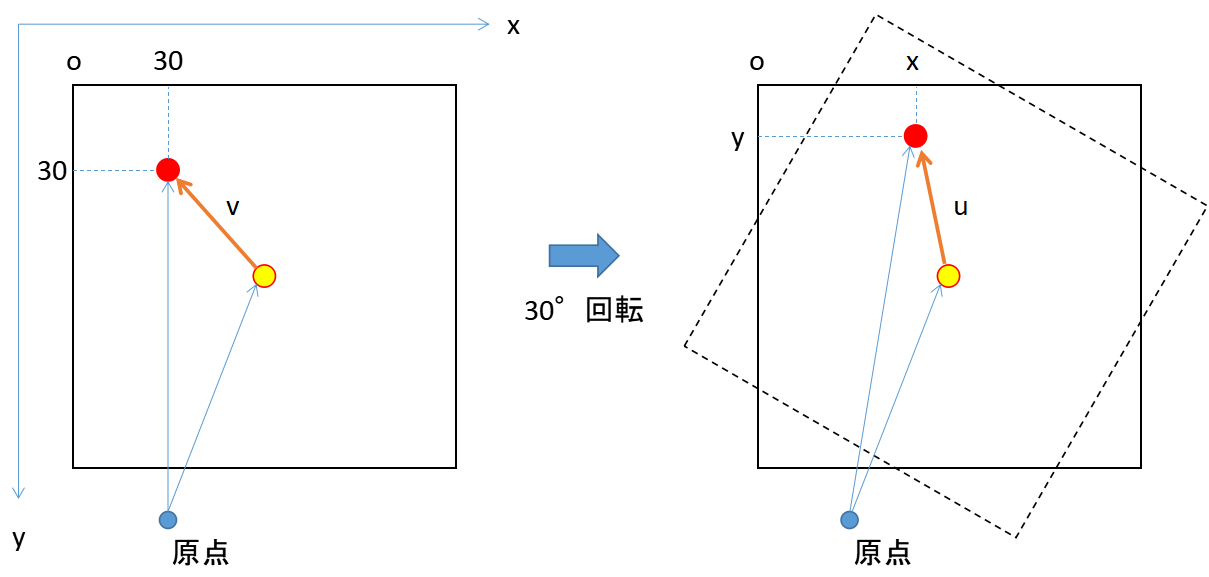
vector1
コードで書くとこのようになります。

# centerからp1までのベクトル
v = p1 - center

# 回転後のベクトル
u = rotCoordinate(v, rad)
uc = u + center

print(uc)
>>[42.67949192 22.67949192]

 

まとめ

今回は回転後の座標を取得する方法を紹介しました。

回転行列を用いると簡単に求めることができましたね。

中学、高校で勉強したことが画像処理の世界で大いに役立つことを日々実感しています。

RELATED POST